Revisiting Event Study Designs

That is a working paper by Borusyak and Jaravel on SSRN. The paper looks at an underidentification problem in event study designs, where all units in the data eventually receive the treatment at the same time (i.e. there is no control group).

Since there is no control group, one way to check the validity of such an approach rests is to check that there is not pre-trend before the treatment occurs, much like the parallel trends assumption we use for diff-in-diff designs.

A natural way to do this is to estimate the following specification for an individual-year panel:

$\alpha_i$ is an individual fixed effect, $\beta_t$ is a calendar year effect, and $K_{it}$ is a time period relative to that individual’s treatment period, which I’m assuming goes from -5 to 6 (0 is treatment year). Note that

where $t$ is a calendar year and $E_i$ is the year of treatment for individual $i$.

Two things here:

1. $E_i$ is an time-invariant individual level variable so it is accounted for by the individual fixed effect.

2. $K$, $t$, and $E$ are linearly related, and the authors show that in the model, $\gamma_k$ are only identified up to a linear trend. That is, for any set of estimate of $\gamma_k$, you can add a linear trend in $k$ and adjust the individual or year fixed effects to get the same predicted value.¹

More practically, this means that you cannot identify linear trends in $\gamma_k$. If you actually try to estimate the model in R or Stata, the program will drop two of the $k$ categories rather than just one. The interpretation of the coefficients that are returned are deviations from the line between the two categories.

To illustrate, consider an example where the true $\gamma$’s are indeed linear before treatment.

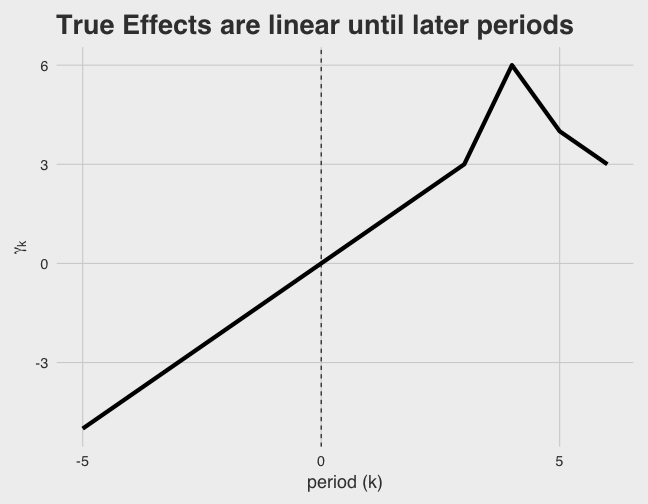
If we drop $k = 0$ and $k = -5$ from the estimation, then what we’re estimating is the deviation from the straight line that joins $\gamma_0$ and $\gamma_{-5}$.

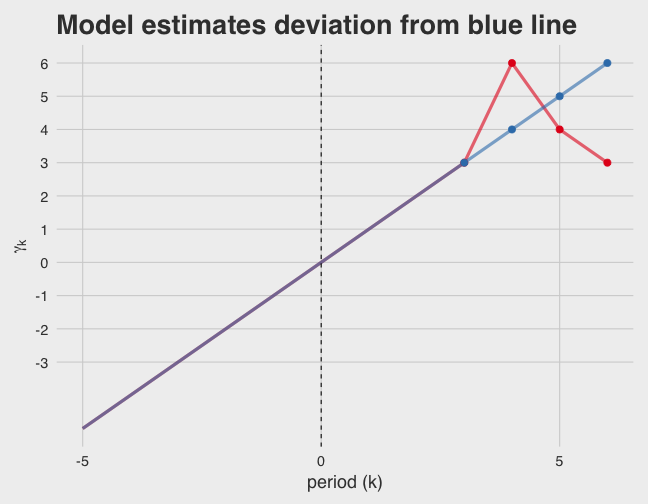
Just to be sure, let’s try actually estimating a very simple example data set with the same “true” effects. ²

# Example dataset with linear pre-trend

nyears = length(periods)

years = c(1991:2002, 1992:2003)

yearfe = data_frame(year = 1991:2003, yearfe = c(rep(5, 10), 3, 1, 2))
idfe = data_frame(id = 1:100, idfe = 0)

df = data_frame(id = rep(1:100, nyears)) %>% arrange(id)

df = df %>% 
  mutate(period = rep(periods, 100), year = rep(years, 50)) %>% 
  left_join(period_coefs, by = 'period') %>% 
  left_join(yearfe, by = 'year') %>% 
  left_join(idfe, by = 'id') %>% 
  mutate(y = yearfe + idfe + effect + rnorm(1200, sd = 0.1))

# Explicit dummy for each period so can choose which to drop
for (i in -5:6){
  if (i >= 0){
    period_i = str_c('period_', i)
  } else {
    period_i = str_c('period_neg_', abs(i))
  }
  df %<>%
    mutate_(.dots = setNames(list(~ period == i), list(period_i))) 
}

# sample function to make writing functions for lfe::felm a little clearer
felm_str = function(y, x, fe, iv, clusters){
  a = str_c(x, collapse = " + ")
  b = str_c(fe, collapse = " + ")
  c = str_c(iv, collapse = " + ")
  d = str_c(clusters, collapse = " + ")
  rhs = str_c(a, b, c, d, sep = " | ")
  model_str = str_c(y, rhs, sep = " ~ ")
  # model = formula(model_str)
  # model = reformulate(rhs, y)
  # return(model_str)
}

f = formula(felm_str('y', c(str_c('period_neg_', 4:1), str_c('period_', 1:6)), c('id', 'year'), '0', '0'))

est = felm(f, data = df)

est_coefs = tidy(est) %>% 
  tidyr::extract(term, 'period', regex = "_([1-9])", remove = FALSE, convert = TRUE) %>% 
  mutate(period = ifelse(str_detect(term, 'neg'), -period, period)) %>%
  bind_rows(data_frame(period = c(0, -5), estimate = 0))

est_coefs %>% 
  ggplot(aes(period, estimate)) + 
  geom_line(size = 1.5, alpha = 0.6, linetype = 2) +
  geom_point(data = filter(est_coefs, period >= 3), size = 3) + 
  geom_vline(xintercept = 0, linetype = 2) + 
  scale_x_continuous(breaks = c(-5, 0, 5)) +
  labs(x = "period (k)", y = quote(hat(gamma[k])), 
       title = "Estimates as deviations from linear trend") +
    scale_colour_brewer(palette = "Set1")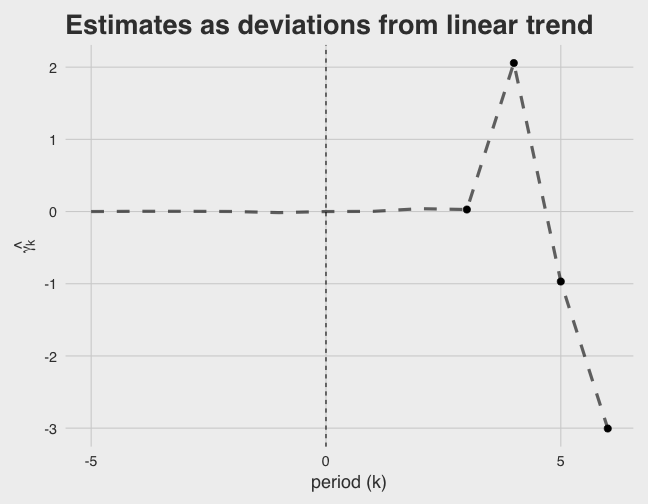

Borusyak and Jaravel propose a couple of ways to approach this problem. In brief,

1. Estimate two models: the full model, and a “semi-dynamic model” where $\gamma_k = 0$ for all $k$, and run an F-test on both models.

2. Use individual random effects (they also propose a Hausman test using the result that random effects is more efficient than fixed effects).

I’ll probably do a later post on these when I’ve (a) thought more about how they would fit into a project and (b) figured out how to implement them in R.

There’s more in the paper besides the pre-trend discussion that should be of interest to applied micro researchers, such as estimating time-varying effects versus a single effect for all post-treatment periods.